pyAB¶

pyAB is a Python package for Bayesian & Frequentist A/B Testing.

Features:¶

Bayesian A/B Test:

Conduct quick experiments to check for winning variant with additional prior information (Beta Distribution parameters).
Try different evaluation metrics (Uplift Ratio, Uplift Difference & Uplift Percent Gain) & vary number of mcmc simulations.
Visualize & inspect Uplift Density & Cumulative Density distributions.

Frequentist A/B Test:

Conduct quick experiments to check for winning variant using two sample proportion test (Statistical significance).
Estimate required sample size per variant to reach provided Type-II error rate.
Visualize & inspect power curve for varying alternative proportions.

Content

Usage:¶

Bayesian A/B Test¶

Let us assume we have two Banner Ads and want to run an AB Test to decide on the final version. We run the test and collect 1000 samples per version. We observe 100 and 120 clicks for version-A & Version-B respectively (10 % & 12.5 % Click-through-rates). From our previous experience, we know that the average Click-through-rate for our previous Ads was around 12 %.

We first need to import ABTestBayesian class and provide prior clicks success_prior and prior impressions trials_prior. Then, call the conduct_experiment method with successful clicks and impressions per version.

For uplift_method, there are three metrics to choose from are 'uplift_ratio', 'uplift_percent' & 'uplift_difference'. We also choose mcmc num_simulations, which samples from Uplift Probability Density function.

# import Bayesian class
from pyab.experiments import ABTestBayesian

# provide beta priors
ad_experiment_bayesian = ABTestBayesian(success_prior=120, trials_prior=1000)

# conduct experiment with two variants successes and trials, along with uplift method and number of simulations
ad_experiment_bayesian.conduct_experiment(success_null=100, trials_null=1000,
                                          success_alt=125, trials_alt=1000,
                                          uplift_method='uplift_ratio', num_simulations=1000)

Bayesian A/B test results can extremely useful to understand & communicate test results with other stakeholders and answers the main business question: Which version works the best ?

Output:

pyAB Summary
============

Test Parameters
_______________

Variant A: Successful Trials 100, Sample Size 1000
Variant B: Successful Trials 125, Sample Size 1000
Prior: Successful Trials 120, Sample Size 1000

Test Results
____________

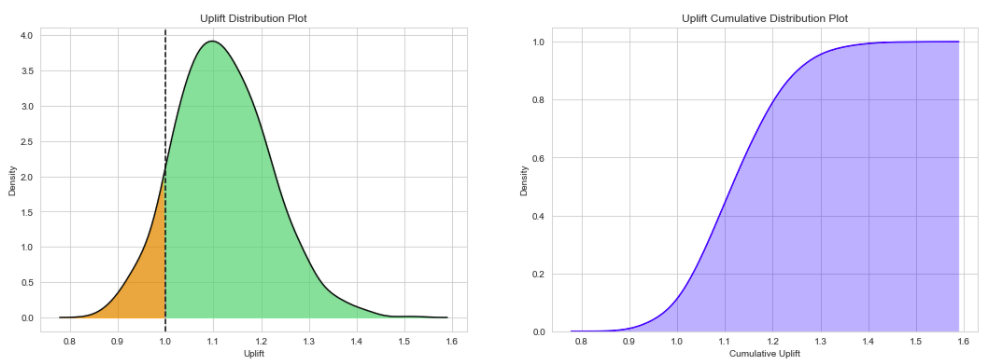
Evaluation Metric: uplift_ratio
Number of mcmc simulations: 1000

90.33 % simulations show Uplift Ratio above 1.

Frequentist A/B Test¶

Let us now run a Frequentist A/B Test and verify if there is a significant difference between two proportions provided the sample sizes and Type-I Error rate. From above, we know the performance of version-A & version-B (10 % & 12.5 % Click-through-rates), for 1000 impressions of each version.

We first need to import ABTestFrequentist class and provide type of alternative hypothesis alt_hypothesis, 'one_tailed' or 'two_tailed' & Type-I error rate alpha (default = 0.05). Then, we call the conduct_experiment method with successful clicks and impressions per version.

This traditional methodology might be slightly tricky to communicate, and Type-I & Type-II error rates need to be accounted for, unlike Bayesian methods.

# import Frequentist class
from pyab.experiments import ABTestFrequentist

# provide significance rate and type of test
ad_experiment_freq = ABTestFrequentist(alpha=0.05, alt_hypothesis='one_tailed')

# conduct experiment with two variants successes and trials, returns stat & pvalue
stat, pvalue = ad_experiment_freq.conduct_experiment(success_null=100, trials_null=1000,
                                 success_alt=125, trials_alt=1000)

Output:

pyAB Summary
============


Test Parameters
_______________

Variant A: Success Rate 0.1, Sample Size 1000
Variant B: Success Rate 0.125, Sample Size 1000
Type-I Error: 0.05, one_tailed test


Test Results
____________

Test Stat: 1.769
p-value: 0.038
Type-II Error: 0.451
Power: 0.549

There is a statistically significant difference in proportions of two variants.

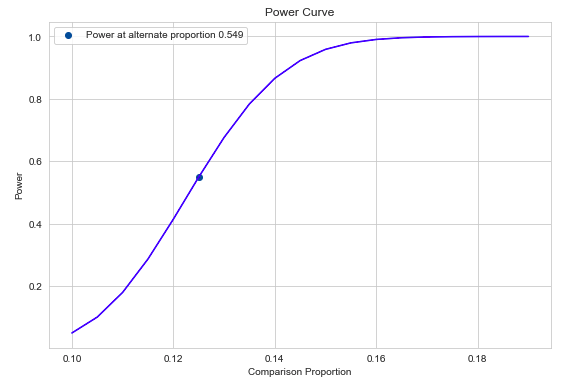
Given that the current Type-II error is 0.451 at 1000 samples per variant, we can find out required sample size per variant to reach Type-II error of 0.1.

# required sample size per variant for given beta
ad_experiment.get_sample_size(beta=0.1)

Output:

Never misinterpret your Results !